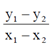Pendekatan Kontekstual Pada Materi
Persamaan Garis Lurus Sebagai Implementasi Teori Belajar Brunner Dan Piaget Berbantuan
Geogebra
ABSTRAK
Persamaan
garis lurus merupakan salah satu materi yang dipelajari siswa SMP kelas VII.
Dalam persamaan garis lurus hal yang dipelajari adalah bagaimana menentukan
gradien suatu garis, menyusun persamaan suatu garis dengan satu atau dua titik
yang diketahui, menentukan hubungan garis-garis yang sejajar dan tegak lurus
satu sama lain. Dalam mempelajari ini, siswa mengalami
kesulitan dalam memberikan makna terhadap gradien dan konstanta suatu garis
lurus. Hal ini bisa dipahami karena memang sebelumnya persamaan garis hanya
diajarkan secara analitik, pendekatan visual masih belum digunakan secara
optimal dalam pembelajaran materi ini. Untuk mengatasi permasalahan tersebut
maka akan dioptimalkan dalam pendeketan visual dalam pengajaran persamaan garis
lurus dengan menerapkan pendekatan kontekstual hal ini dikarenakan pada tahapan
matematisasi horizontal yang menggunakan pendekatan pembeajaran kontekstual
keberadaan multimedia (pendekatan visual) berperan penting. Dalam penerapan pendekatan pembelajaran kontekstual pada materi
persamaan garis lurus ditinjau dari teori belajar brunner yaitu apabila
ditinjau dari teori belajar bruner pendekatan pembelajaran kontekstual telah
cocok diterapkan pada materi persamaan garis lurus karena langkah – langkah
pembelajaran pada pendekatan kontekstual telah sesuai dengan tahapan belajar
yang dikemukakan oleh Bruner.
PENDAHULUAN
Menurut Russeffendi, matematika masih dipandang
sebagai salah satu bidang studi yang sulit dan anggapan bahwa matematika tidak
disenangi atau bahkan paling dibenci, masih saja melekat pada kebanyakan siswa
yang memperlajarinya. Bahkan siswa pun berpendapat bahwa pelajaran matematika
membosankan, tidak menarik, bahkan penuh misteri, sehingga berujung pada hasil
belajar matematika yang rendah. Hasil belajar matematika yang rendah bukan saja
terjadi pada kelas-kelas biasa, tetapi juga pada kelas unggulan. Kemungkinan
hal ini disebabkan kurang bervariasinya situasi pembelajaran. Pembelajaran yang
monoton menerapkan suatu model yang akan mengurangi minat belajar siswa.
Kurangnya minat belajar ini pun akan berpengaruh pada tingkat ketuntasan siswa
dalam menguasai materi yang dipelajari. Karena sifat matematika yang hierarkis,
penguasaan suatu konsep yang tidak tuntas ini secara keseluruhan akan
menimbulkan masalah yang semakin besar. Jika siswa gagal dalam konsep tertentu,
mungkin bukan karena konsep tersebut sulit, melainkan karena ia tidak menguasai
konsep yang mendasarinya.
Menurut Jurnal Pendidikan Indonesia, siswa mengalami
kesulitan dalam memberikan makna terhadap gradien dan konstanta suatu garis
lurus. Hal ini bisa dipahami karena memang sebelumnya persamaan garis hanya
diajarkan secara analitik, pendekatan visual masih belum digunakan secara
optimal dalam pembelajaran materi ini. Banyak ahli media mengemukakan perlu
adanya pemilihan media yang tepat sebagai bahan penyalur pesan dalam proses pembelajaran.
Bahkan diyakini bahwa media audio visual
sangat baik digunakan untuk membantu proses komunikasi di kelas.
Marpaung dalam artikel pembelajaran matematika mengatakan, bahwa
proses pembelajaran matematika di sekolah adalah sebuah proses matematisasi
yang terdiri dari dua proses, yakni matematisasi horisontal dan matematisasi
vertikal. Matematisasi horizontal adalah sebuah proses mentransfer dunia siswa
kedalam dunia matematika. Dalam prakteknya, guru menggunakan pendekatan
pembelajaan kontekstual dimana guru mengawali pembelajaran dari masalah-masalah
kontekstual, untuk kemudian melakukan formalisasi matematis. Sedangkan
matematisasi vertikal adalah sebuah proses pembelajaran matematika formal.
Artinya, setelah melalui proses formalisasi, maka penyelesaian persoalan
matematika selanjutnya menggunakan pendekatan formal. Dalam prakteknya, guru
mengajak siswa untuk menyelesaikan persoalan melalui pendekatan formal. Pada
tahapan matematisasi horizontal inilah keberadaan multimedia berperan penting.
Berdasarkan penjelasan diatas, pada permasalahan persamaan garis
lurus pendekatan yang akan dipakai adalah pendekatan kontekstual hal ini
dikarenakan pendekatan ini akan dapat mengatasi kesulitan siswa dalam memahami
konsep persamaan garis lurus dan akan dikaitkan berdasarkan teori brunner agar
pendekatan yang diberikan lebih mudah diberikan kepada siswa.
MATERI
GRAFIK PERSAMAAN GARIS LURUS
Ø
Gradien Persamaan garis lurus
Dari gambar diatas memuat beberapa garis lurus yang
melalui titik pangkal koordinat. Jika kita perhatikan garis-garis tersebut
mempunyai kemiringan atau kecondongan. Kemiringan dari suatu garis
lurus disebut gradien dari garis
lurus tersebut. Bagaimanakah cara menentukan gradien suatu garis lurus?
Ø
Menentukan
Gradien Lurus
a) Menghitung
Gradien pada Persamaan Garis y = mx.
Seperti yang telah dijelaskan sebelumnya, gradien suatu garis dapat ditentukan melalui perbandingan antara ordinat dan absis sehingga dapat ditulis sebagai berikut.
Dari uraian ini terlihat bahwa nilai gradien dalam suatu persamaan garis sama dengan besar nilai konstanta m yang terletak di depan variabel x, dengan syarat, persamaan garis tersebut diubah terlebih dahulu ke dalam bentuk y = mx.
Seperti yang telah dijelaskan sebelumnya, gradien suatu garis dapat ditentukan melalui perbandingan antara ordinat dan absis sehingga dapat ditulis sebagai berikut.
Dari uraian ini terlihat bahwa nilai gradien dalam suatu persamaan garis sama dengan besar nilai konstanta m yang terletak di depan variabel x, dengan syarat, persamaan garis tersebut diubah terlebih dahulu ke dalam bentuk y = mx.
b)
Menghitung Gradien pada Persamaan
Garis y = mx + c
Sama halnya dengan perhitungan gradien
pada persamaan garis y = mx, perhitungan gradien pada garis y = mx + c
dilakukan dengan cara menentukan nilai konstanta di depan variabel x.
c)
Menghitung Gradien pada Persamaan
Garis ax + by + c = 0
Sama seperti sebelumnya, gradien
pada persamaan garis ax + by + c = 0 dapat ditentukan dengan cara mengubah
terlebih dahulu persamaan garis tersebut ke dalam bentuk y = mx + c. Kemudian,
nilai gradien diperoleh dari nilai konstanta m di depan variabel x.
d) Menghitung Gradien pada Garis yang Melalui Dua Titik
Coba kamu perhatikan Gambar 3.5 berikut.
Gambar 3.5 menunjukkan tiga buah segitiga ABC, DEF, dan GHI yang memiliki sisi miring dengan tingkat kemiringan atau gradien yang berbeda-beda. Dengan menggunakan perbandingan ordinat dan absis, gradien untuk masing-masing segitiga dapat dihitung.
PENDEKATAN
KONTEKSTUAL
Trianto menyatakan bahwa Pendekatan Kontekstual
merupakan konsep belajar yang membantu guru mengaitkan antara materi yang
diajarkan dengan situasi dunia nyata siswa dan mendorong siswa membuat hubungan
antara pengetahuan yang dimilikinya dengan penerapan dalam kehidupan mereka
sebagai anggota keluarga dan masyarakat. Dengan konsep itu, hasil pembelajaran
yang diharapkan lebih bermakna bagi siswa. Proses pembelajaran berlangsung
alamiah dalam bentuk kegiatan siswa bekerja dan mengalami, bukan mentransfer
pengetahuan dari guru ke siswa. Strategi pembelajaran lebih dipentingkan
daripada hasil.
Pendekatan
kontekstual mendasarkan diri pada kecenderungan pemikiran tentang belajar
sebagai berikut:
1. Proses belajar
·
Belajar tidak hanya sekedar
menghafal. Siswa harus mengkonstruksikan di benak mereka sendiri.
·
Anak belajar dari pengalaman. Anak
mencatat sendiri pola-pola bermakna dari pengetahuan baru, dan bukan diberi
begitu saja oleh guru.
·
Para ahli sepakat bahwa pengetahuan
yang dimiliki seseorang itu terorganisasi dan mencerminkan pemahaman yang mendalam
tentang suatu persoalan.
·
Pengetahuan tidak dapat
dipisah-pisahkan menjadi fakta-fakta atau proposisi yang terpisah, tetapi
mencerminkan keterampilan yang dapat diterapkan.
·
Manusia mempunyai tingkatan yang
berbeda dalam menyikapi situasi baru.
·
Siswa perlu dibiaskan menyelesaikan
masalah, menemukan sesuatu yang berguna bagi dirinya, dan bergelut dengan
ide-ide.
·
Proses belajar dapat mengubah
struktur otak. Perubahan struktur otak itu berjalan terus seiring dengan
perkembangan organisasi pengetahuan dan keterampilan seseorang.
2. Transfer Belajar
·
Siswa belajar dari mengalami
sendiri, bukan dari pemberian orang lain.
·
Keterampilan dan pengetahuan itu
diperluas dari konteks yang terbatas (sedikit demi sedikit).
·
Penting bagi siswa tahu untuk apa
dia belajar dan bagaimana ia menggunakan pengetahuan dan keterampilan itu.
3. Siswa sebagai pelaku belajar
·
Manusia mempunyai kecenderungan
untuk belajar dalam bidang tertentu, dan seorang anak mempunyai kecenderungan
untuk belajar dengan cepat hal-hal yang baru.
·
Strategi belajar itu penting. Anak
dengan mudah mempelajari sesuatu yang baru. Akan tetapi, untuk hal-hal yang
sulit, strategi belajar amat penting.
·
Peran orang dewasa (guru) membantu
menghubungkan antara yang baru dan yang sudah diketahui.
·
Tugas guru memfasilitasi agar
informasi baru bermakna, memberi kesempatan kepada siswa untuk menemukan dan
menerapkan ide-ide mereka sendiri, dan menyadarkan siswa untuk menerapkan
strategi mereka sendiri.
4. Pentingnya lingkungan belajar
·
Belajar efektif itu dimulai dari
lingkungan belajar yang berpusat pada siswa. Dari guru akting di depan kelas,
siswa menonton ke siswa akting bekerja dan berkarya, guru mengarahkan.
·
Pembelajaran harus berpusat pada
bagaimana cara siswa menggunakan pengetahuan baru mereka. Strategi belajar
lebih dipentingkan dibandingkan hasilnya.
·
Umpan balik amat penting bagi siswa,
yang berasal dari proses penilaian yang benar.
·
Menumbuhkan komunitas belajar dalam
bentuk kerja kelompok itu penting.
Secara garis
besar langkah-langkah penerapan CTL dalam kelas sebagai
berikut :
berikut :
1. Kembangkan pemikiran bahwa anak akan
belajar lebih bermakna dengan
cara bekerja sendiri, menemukan sendiri, dan mengkonstruksi sendiri
pengetahuan dan keterampilan barunya.
cara bekerja sendiri, menemukan sendiri, dan mengkonstruksi sendiri
pengetahuan dan keterampilan barunya.
2. Laksanakan sejauh mungkin kegiatan
inkuiri untuk semua topik.
3. Kembangkan sifat ingin tahu siswa
dengan bertanya.
4. Ciptakan masyarakat belajar (belajar
dalam kelompok-kelompok).
5. Hadirkan semua model sebagai contoh
pembelajaran.
6. Lakukan refleksi di akhir pertemuan.
7. Lakukan penilaian yang sebenarnya
dengan berbagai cara.
TEORI-TEORI
BELAJAR
a.
Teori Belajar BRUNER
Menurut Bruner, dalam
proses belajar dapat dibedakan tiga fase yakni ;
1) Informasi
2) Transformasi
3) Evaluasi
(pengkajian pengetahuan).
Informasi, dalam tiap
pelajaran kita peroleh sejumlah informasi ada yang menambah pengetahuan yang
telah kita miliki, ada yang memperhalus dan memperdalamnya, ada pula informasi
yang bertentangan dengan apa yang telah kita ketahui sebelumnya, misalnya bahwa
tidak ada energi yang lenyap. Transformasi, informasi itu harus dianalisis
diubah atau ditransformasi kedalam bentuk yang lebih abstrak atau konseptual
agar dapat digunakan untuk hal-hal yang lebih luas. Dalam hal ini bantuan guru
sangat diperlukan.
Evaluasi, kemudian
kita nilai hingga manakah pengetahuan yang kita peroleh dan transformasi itu
bisa dimanfaatkan untuk memahami gejala-gejala lain. Dalam proses belajar,
ketiga fase tersebut selalu ada. Yang menjadi masalah ialah berapa banyak
informasi yang diperlukan agar dapat ditransformasikan. Lama tiap episode tidak
selalu sama. Hal ini antara lain juga bergantung pada hasil yang diharapkan,
motivasi murid belajar, minat, keinginan untuk mengetahui dan dorongan untuk
menemukan sendiri.
Teori belajar bruner
dikenal dengan tiga tahapan belajarnya, yaitu enaktif, ikonik dan simbolik.
Pada dasarnya setiap individu pada waktu mengalami atau mengenal peristiwa yang
ada di dalam lingkungannya dapat menemukan cara untuk menyatakan kembali
peristiwa tersebut di dalam pikirannya, yaitu suatu model mental tentang
peristiwa yang dialaminya. Hal tersebut adalah proses belajar yang terbagi
menjadi tiga tahapan, yakni:
1) Tahap enaktif;
dalam tahap ini peserta didik di dalam belajarnya menggunakan atau memanipulasi
obyek-obyek secara langsung.
2) Tahap ikonik; pada
tahap ini menyatakan bahwa kegiatan anak-anak mulai menyangkut mental yang
merupakan gambaran dari objek-objek. Dalam tahap ini, peserta didik tidak
memanipulasi langsung objek-objek, melainkan sudah dapat memanipulasi dengan
menggunakan gambaran dari objek. Pengetahuan disajikan oleh sekumpulan
gambar-gambar yang mewakili suatu konsep.
3) Tahap simbolik;
tahap ini anak memanipulasi simbol-simbol secara langsung dan tidak ada lagi
kaitannya dengan objek-objek. Anak mencapai transisi dari pengguanan penyajian
ikonik ke penggunaan penyajian simbolik yang didasarkan pada sistem berpikir
abstrak dan lebih fleksibel. Dalam penyajian suatu pengetahuan akan dihubungkan
dengan sejumlah informasi yang dapat disimpan dalam pikiran dan diproses untuk
mencapai pemahaman.
Bruner berpendapat
bahwa pengajaran dapat dianggap sebagai;
a) hakikat
seseorang sebagai pengenal
b) hakekat
dari pengetahuan, dan
c) hakekat
dari proses mendapatkan pengetahuan.
Manusia sebagai
makhluk yang paling mulia diantara makhluk-makhluk lain memiliki dua kekuatan
yakni akal pikirannya dan kemampuan berbahasa. Dengan dua kemampuan tersebut
maka manusia dapat mengembangkan kemampuan yang ada padanya. Dorongan dan
hasrat ingin mengenal dan mengetahui dunia dan lingkungan alamnya menyebabkan
manusia mempunyai kebudayaan dalam bentuk konsepsi, gagasan, pengetahuan,
maupun karya-karyanya. Kemampuan yang ada dalam dirinya mendorongnya untuk
mengekspresikan apa yang telah dimilikinya. Kondisi dan karakteristik tersebut
hendaknya melandasi atau dijadikan dasar dalam mengembangkan proses pengajaran.
Dengan demikian guru harus memandang siswa sebagai individu yang aktif dan
memiliki hasrat untuk mengetahui lingkungan dan dunianya bukan semata-mata
makhluk pasif menerima apa adanya.
b. Teori
Belajar Piaget
Teori
perkembangan piaget merupakan teori konstruktivisme, yang memandang
perkembangan kognitif sebagai suatu proses dimana anak secara aktif membangun
sistem makna dan pemahaman realitas melalui pengalaman dan interaksi mereka.
Menurut
piaget setiap individu pada saat tumbuh mulai dari bayi yang baru dilahirkan
sampai menginjak usia dewasa mengalami empat tahap perkembangan kognitif yaitu
sebagai berikut :
a.
Tahap
Sensorimotor (umur 0 – 2 tahun)
Pada
tahap ini terbentuknya konsep “kepermanenan objek” dan kemajuan dari perilaku
yang refleksif ke perilaku yang mengarah kepada tujuan.
a.
Tahap
Pra
Operasional (2 – 7 tahun)
Pada
tahap ini perkembangan kemampuan menggunakan simbol untuk menyatakan objek –
objek dunia. Pemikiran anak pada tahap ini masih egosentris dan sentrasi.
b.
Tahap Operasi Konkret
(7 – 11 tahun)
Pada
tahap ini dinyatakan
dengan perkembangan sistem pemikiran yang didasarkan pada peristiwa-peristiwa
yang langsung dialami. Anak masih menerapkan logika berpikir pada barang-barang
yang konkret, belum bersifat abstrak maupun hipotesis.
c. Tahap
Operasi Formal (11 tahun – dewasa)
Pada
tahap ini merupakan
tahap akhir dari perkembangan kognitif
secara kualitas. Pada tahap ini anak mampu bernalar tanpa harus berhadapan dengan objek
atau peristiwanya langsung, dan menarik kesimpulan dan informasi yang tersedia.
Masalah–masalah dapat dipecahkan melalui penggunaan eksperimentasi sistematik.
Kecepatan
perkembangan tiap individu melalui urutan tiap tahap ini, berbeda dan tidak ada individu yang melompati
salah satu dari tahap diatas. Tiap tahap ditandai dengan munculnya
kemampuan-kemampuan intelektual baru yag memungkinkan orang memahami dunia
dengan cara yang semakin kompleks.
KETERKAITAN PENDEKATAN
KONTEKSTUAL DENGAN TEORI BRUNNER DAN PIAGET PADA PERSAMAAN GARIS LURUS
Persamaan garis lurus merupakan salah satu materi yang dipelajari siswa SMP
kelas VII. Dalam persamaan garis lurus hal yang dipelajari adalah bagaimana
menentukan gradien suatu garis, menyusun persamaan suatu garis dengan satu atau
dua titik yang diketahui, menentukan hubungan garis-garis yang sejajar dan
tegak lurus satu sama lain. Dalam mempelajari ini, siswa
mengalami kesulitan dalam memberikan makna terhadap gradien dan konstanta suatu
garis lurus. Hal ini bisa dipahami karena memang sebelumnya persamaan garis
hanya diajarkan secara analitik, pendekatan visual masih belum digunakan secara
optimal dalam pembelajaran materi ini. Untuk mengatasi permasalahan tersebut
maka akan dioptimalkan pendeketan visual dalam pengajaran persamaan garis lurus
dengan menerapkan pendekatan kontekstual hal ini dikarenakan pada tahapan
matematisasi horizontal yang menggunakan pendekatan pembeajaran kontekstual keberadaan
multimedia (pendekatan visual) berperan penting. Hal ini dikarenakann
multimedia memiliki potensi dan
kemampuan yang dapat dimanfaatkan untuk membantu proses tersebut diantaranya;
1) Membuat konsep yang abstrak menjadi kongkrit.
2) Menampilkan animasi baik berupa gerakan maupun
suara yang mengilustrasikan proses yang terjadi.
3) Mampu memberikan keseragaman persepsi, karena
media mampu dimanfaatkan untuk memfokuskan perhatian siswa.
4) Mampu menyajikan informasi belajar secara
konsisten dan dapat diulang kapan dan dimanapun.
5) Mampu mengatasi keterbatasan waktu dan tempat
belajar.
Dengan dioptimalkannya pendekatan visual melalui
pendekatan kontekstual ini tentu adanya perantara dalam penggunaannya, dalam
hal ini perantaranya adalah komputer. Feedback
yang diberikan
komputer baik dalam bentuk angka maupun grafik dan animasi bersifat sangat
segera, ini merupakan suatu hal yang sulit diperoleh sebelumnya dengan tanpa menggunakan
komputer. Inilah yang menyebabkan orang-orang berpikir mengapa pembelajaran
berbantuan komputer kemungkinan besar akan dapat meningkatkan motivasi belajar
dan pada gilirannya meningkatkan hasil belajar. Hal ini selaras dengan apa yang
dikatan pada Jurnal Pendidikan Indonesia, pendekatan baru dalam pembelajaran
matematika menggunakan apa yang disebut dengan pendekatan aturan 3 (the
rule of three), yakni sedapat mungkin konsep-konsep matematika harus
disajikan dengan menggunakan tiga pendekatan yaitu analitik, numerik, dan
visual. Tujuannya adalah agar konsep-konsep matematika bisa dilihat dari
berbagai sudut dan dengan demikian memperbesar peluang konsep tersebut bisa
dimengerti oleh siswa yang karakteristiknya bervariasi. Sebagai contoh adalah
pembelajaran konsep gradien suatu garis lurus. Secara analitik, tentu saja
gradien garis lurus yang melalui titik-titik (x1,y1) dan
(x2,y2) adalah harga dari:
Jika hanya ini yang disampaikan ke siswa, maka
mereka akan menghafal saja rumus tersebut. Tetapi, jika gradien juga disajikan
secara visual, maka kemungkinan besar rumus tersebut akan dapat dimengerti
dengan lebih baik oleh lebih banyak siswa. Demikian juga halnya dengan konsep
kesejajaran, ketegaklurusan, dan keberpotongan antara dua garis lurus akan
lebih mudah dimengerti jika disajikan secara visual. Piaget
mengungkapkan bahwa usia siswa SMP masih berada dalam tahapan operasional
formal. Namun demikian, meski pada usia tersebut siswa sudah mampu berfikir
logis tanpa kehadiran benda kongkrit, akan tetapi kemampuan siswa untuk
berfikir abstrak masih belum berkembang dengan baik, sehingga dalam beberapa
hal kehadiran peraga atau media belajar lainnya masih dibutuhkan. Oleh karena
itu untuk mengajarkan materi persamaan garis lurus ini guru akan menggunakan
media pembelajaran berupa aplikasi Geogebra. Hal ini
dikarenakan geogebra merupakan program komputer yang kini tersedia secara luas
dan gratis di internet.
Dari gambar tersebut dapat dihitung kemiringan dari AB dengan cara membagi
perubahan titik secara vertikal dengan perubahan titik secara horizontal.
Selanjutnya untuk melihat apakah di titik yang berbeda pada garis tersebut akan diperoleh nilai kemiringan yang sama, dapat dibuatkan sebuah titik baru di garis tersebut misalnya titik (0,3) maka dapat diperoleh kesimpulan bahwa kemiringannya adalah tetap. Nilai kemiringan inilah yang disebut gradien. Apabila kita tinjau dari teori brunner, pembelajaran menggunakan visual ini sangat cocok diterapkan dalam memahami konsep gradien. Dimana menurut brunner ada tiga tahap pembelajaran, yaitu ;
1. Tahap
enactive
Pada tahap ini siswa dapat melihat
bagaiman kemiringan garis yang ditentukan oleh gradien.
2. Tahap
ikonik
Pada tahap ini, siswa telah dapat
membayangkan bagaimana konsep dari gradien tersebut.
3. Tahap
symbolik
Pada tahap ini, siswa telah dapat
menuliskan konsep gradien dengan menggunakan simbol-simbol matematika.
DAFTAR PUSTAKA
Ikhsanudin. (2010, Oktober). Belajar Geogebra.
Dipetik November 2016, dari Blogspot: http://googebra.blogspot.co.id/2014/10/menentukan-gradien-sebuah-garis.html
MUTAQIN, H. Z. (2012, November 1). Artikel Pembelajaran
Matematika. Dipetik Oktober 12, 2016, dari Blogspot:
http://artikel-pembelajara.blogspot.co.id/2012/11/persamaan-garis-lurus.html?m=1
Ruseffendi, E. (1998). Dasar-Dasar Matematika Modern
untuk Guru, Edisi Ketiga. Bandung: Tarsito.
Suweken, G. (2013). PENGINTEGRASIAN MEDIA PEMBELAJARAN
VIRTUAL BERBASIS GEOGEBRA UNTUK MENINGKATKAN KETERLIBATAN DAN PEMAHAMAN
KONSEP MATEMATIKA SISWA KELAS VIII SMPN 6 SINGARAJA. Jurnal Pendidikan
Indonesia , 2-4.