Resume
Materi Matriks
1)
Matriks
Definisi
1.1
Matriks merupakan susunan skalar elemen-elemen dalam bentuk baris dan kolom.
Matriks berukuran m × n dengan m baris dan n kolom.
Entri aij disebut elemen matriks pada
baris ke-i dan kolom ke-j. Jika m = n maka matriks tersebut dinamakan matriks
bujursangkar (square matrix). Matriks
biasa dilambangkan dengan [ ] atau ( ).
Beberapa
matriks khusus
a. Matriks
diagonal
Matriks diagonal merupakan matriks bujursangkar
dengan aij = 0 untuk i ≠ j. Dengan kata lain, seluruh elemen yang
tidak terdapat pada posisi i ≠ j bernilai 0
Contoh
Di bawah ini adalah contoh-contoh matriks yang
berukuran 3 × 3 dan 2 × 2.
b. Matriks
Indentitas
Matriks identitas merupakan matriks bujursangkar
dengan semua elemen diagonal bernilai 1 dan elemen lainnya bernilai 0. Matriks
ini dilambangkan dengan I.
Contoh
Di
bawah ini adalah contoh- contoh matriks yang berukuran 3 × 3 dan 2 × 2.
c. Matriks
segitiga atas atau bawah
Matriks segitiga atas merupakan matriks bujursangkar dengan
elemen matriks aij = 0 untuk i > j atau
elemen-elemen matriks di bawah diagonal utama bernilai 0. Sedangkan, matriks
segitiga bawah merupakan matriks bujursangkar dengan
elemen matriks aij = 0 untuk i < j atau
elemen-elemen matriks di atas diagonal utama bernilai 0.
Contoh
Di
bawah ini adalah contoh- contoh matriks segitigas atas dan matriks segitiga
bawah yang berukuran 3 × 3.
d. Matriks
traspose
Matriks trasnpose
merupakan matriks yang diperoleh dengan menukarkan baris-baris dan kolom-kolom.
Matriks ini dilambangkan dengan AT.
Contoh
Di
bawah ini adalah contoh matriks transpose
(AT) dari matriks A yang berukuran 3 × 3.
e. Matriks
setangkup
Matriks setangkup merupakan matriks dimana elemen
yang berada di atas diagonal nya adalah hasil pencerminan dari elemen yang
berada di bawah diagonal nya. Dengan kata lain, bagian atas dan bawah dari
diagonal adalah sama. Dikatakan matriks setangkup jika matriks AT =
A.
Contoh
Di
bawah ini adalah contoh matriks setangkup dari matriks A yang berukuran 3 × 3.
f. Matriks
0/1
Matriks 0/1 merupakan matriks yang elemen-elemen nya
hanya bernilai 0 atau 1.
Contoh
Di
bawah ini adalah contoh - contoh matriks 0/1 yang berukuran 3 × 3 dan 2 × 2.
Operasi Matriks
a. Penjumlahan
dua buah matriks
Dua buah matriks dapat dijumlahkan jika memiliki
jumlah baris dan kolom yang sama.
b. Perkalian
dua buah matriks
Dua buah matriks dapat dikalikan jika memiliki
jumlah ordo baris pada matriks 1 sama dengan ordo kolom pada matriks 2. Artinya
Am × r × Br × n = Cm × n .
Sifat-sifat
operasi perkalian matriks :
1.
Pekalian matriks tidak komutatif,
yaitu AB ≠ BA
2.
Sifat asoasiatif berlaku pada operasi perkalian
matriks : (AB)C = A(BC)
3.
Sifat distributif berlaku pada operasi perkalian
matriks :
· A(B + C) =
AB + AC (sifat distributif kiri)
· (A+B) C = AC
+ BC (sifat distributif kanan)
4.
Perkalian matriks dengan matriks
identitas tidak mengubah matriks, yaitu AI
= IA = A
5.
Perpangkatan matriks didefinisikan
sebagai berikut :
6.
A adalah matriks ortogonal jika AAT
= ATA = I
c. Perkalian
matriks dengan skalar
Perkalian matriks dengan skalar dilakukan dengan
mengalikan semua elemen pada matriks A dengan k.
Sumber : Munir, Rinaldi, Matematika Diskrit, Penerbit Informatika, 2005.






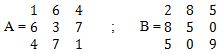



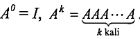






0 komentar:
Posting Komentar